Date Range: November 1 – November 5
Hours Spent:
14 hours –
- 5 hours on lectures and notes Professor Leonard – Calculus 2 Lecture 9.2: Series, Geometric Series, Harmonic Series, and Divergence Test (Calculus 2 Lecture 9.2: Series, Geometric Series, Harmonic Series, and Divergence Test)
- I watch the lecture and scratch out notes, then after I’ve finished I go slowly through my notes and rewrite them neatly into a different notebook. This second notebook is kept for longer-term reference. This also helps the lecture sink in
- 9 hours on exercises (Thomas 13th ed, questions 1 – 55)
- Summary:
- Whereas the previous section looked at the new concept of sequences, this section addressed the sum of sequences, i.e. series, and the convergence/divergence thereof. We learn that we can take partial sums of our series, ascertain their respective formulas, and then take the limits of those to find convergence/divergence of both the partial sums and the series from which they were derived.
- Series come in different forms – at least it helps us to categorize them as such so we can operate on them more easily.
We’re introduced to telescoping series, e.g. n=1[1/(2n+3) – 1/(2n + 1)] which result in partial sums made up of the first and last terms of the respective partial series.
A lot of attention is given to the evaluation of geometric series, i.e. n = 1arn-1. Basically, these are series where the ratios of consecutive terms are constant. While this makes sense to me, I’ll admit I was tripped up a few times in identifying 1) if a series was geometric, and 2) distinguishing the a and r.
We also briefly touched on harmonic series where their terms become something like 1 + ½ + ⅓ + ¼ ….
So with all of these I practiced a lot of 1) determining whether a series is convergent, and if it is 2) finding its sum. Rather than learn new tools, like is often the case throughout Calculus 2, I applied familiar tools (particularly algebra and limits) to the newly aforementioned concepts.
Personal Observations:
- Much of this, like with the previous section, is intuitive for me. I’m often able to determine rather quickly whether a series is convergent or not.
- Problems like this can be a real time consuming pain in the ass:
The reason is not so much finding convergence, but the partial fraction calculation inherent to the problem. Look at this cobweb of an answer:
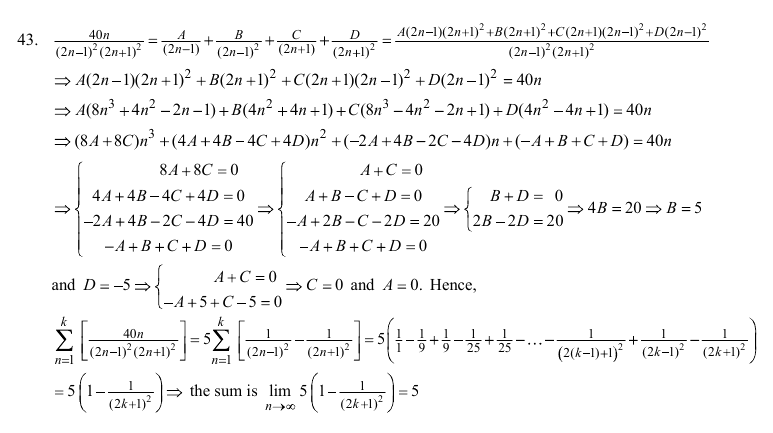
Reflections:
My kneejerk reaction to a problem like that above is to pass it by. I know it’ll take time and I’ll likely bungle it because of poor penmanship or poor organization of my variables. But then I stopped, thought about that reaction, and went to work solving the problem precisely because it elicited such a kneejerk response. It’s important that I don’t fall into the path-of-least-resistance mentality. Furthermore, there are so many concepts packed into Calculus, I should spend more time reviewing old concepts like this. So I churned it and came out with butter, and felt better for doing so.