Integration by Parts (IDP) is a means of integration products of functions that can’t be solved through simple antiderivation or u-substitution. We use it to simplify said product into something that’s easier to integrate. The formula for integration by parts is as follows:
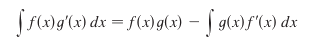
Although what is more readily remembered and used when grinding through problem sets is:
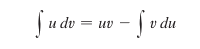
The simpler problems that would have previously given us problems with our rudimentary integration tool are a snap. Something like this, for example:
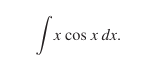
Some trickier problems draw us into cyclic integration by parts, i.e. when the integrals we start with reappear in the equation, such as happens in a problem like this:
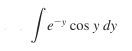
These are pretty easily overcome with some substitution magic tricks – lots of fun.
We also add on tabular integration here, which is a “I should have seen that sooner” kind of tool that lets us easily dispatch of integrations by deriving f(x), integrating g(x), and multiplying multiplying those together (+, – alternating) until f(x) derives to 0.
Finally, we learn the Reduction Formula for finding integrals of sin(x) and cos(x) to the n power. These formulas and identities keep piling up. I keep a notebook handy so they’ll all be handy, but I think I need to memorize them all for more efficient problem solving.
Like with much of Calculus thus far, the greatest difficulty is in minding the details and the tedium of algebra. And, like with all of the challenges thus far, the key is practice, grinding out problem after problem until one goes from 30 minutes to 5 minutes, to the point that it makes sense and is simply formulaic. So, onward I grind…