Calculus 2 thus far has been, in a nutshell, “I know how to integrate these, that, and those, but I don’t yet know how to integrate this – so let’s learn how.” Then, through each successive unit or lesson, I climb up another run of the shoulders-of-giants ladder by learning a new integration tool. This rung, Integration by Partial Fractions, enables me to decompose rational fractions into a sum of fractions that can more easily be integrated with pre-existing integration tools (e.g. u-substitution, trigonometric substitution, integration by parts, etc).
Basically, we take polynomials over polynomials that we run through the algebra gristmill to factor into their most reducible elements. Then we integrate those elements. Those elements are either linear factors (e.g. x + 1) or quadratic factors (e.g. x2+ 1). These polynomials/polynomials come in four flavors, or cases, that are each solved in a different manner:
Case 1 – Polynomials which can be factored into a product of distinct linear factors. Take for example:
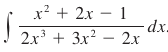
The denominator is factored into x, (2x – 1), and (x + 2), as such:
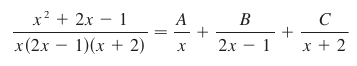
We use basic algebra to solve for A, B, and C, so A = ½, B = ⅕ , and C = -1/10. From here, it’s easy plug-and-play integration:
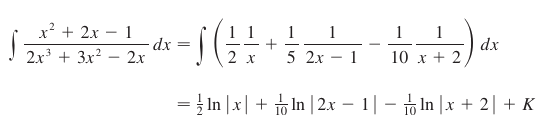
Case 2 – Polynomials which can be factored into a product containing repeated linear factors.
Take for example:
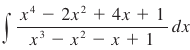
The denominator is factored into (x – 1)² ( i.e. (x – 1)(x – 1) ), and (x + 1). Thus, we decompose our function like this:
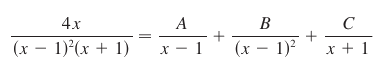
We can then solve for A, B, and C: A = 1, B = 2, C = -1. From here it’s smooth-sailing integration:
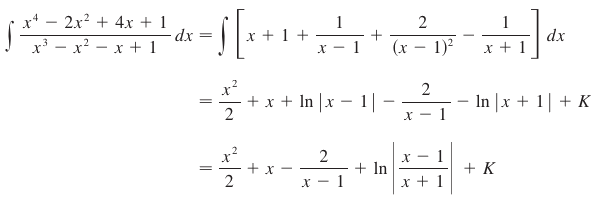
Case 3 – Polynomials which contain irreducible quadratic factors.
Take for example:
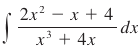
Here, we can’t factor the denominator into simple linear factors. Instead, it factors into x and (x2 + 4) and decomposes to:
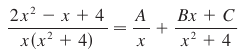
OK, no problem. We solve for A, B, and C, so A = 1, B = 1, and C = -1. We plug those figures in, consult our growing mental rolodex of identities, and voila:
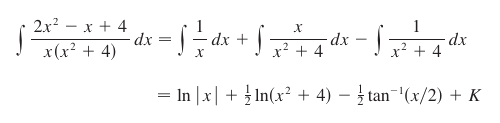
Case 4 – Polynomials which contain repeated irreducible quadratic factors.
Take for example:
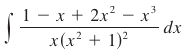
No big deal, we combine the previous approaches, decompose, and solve. So
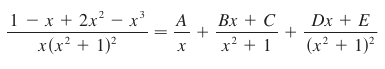
becomes
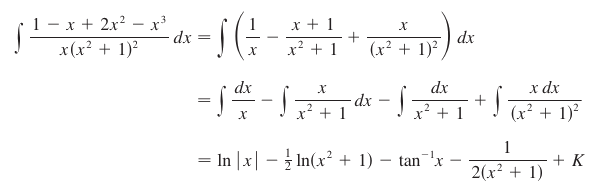
None of these are difficult to process. Having done umpteen hundred integration problems already, we know our algebra, we know how to integrate. We might have a list of identities and other tricks handily nearby. Integration by Partial Fractions is just old ingredients mixed up into a new stew. Where it becomes difficult is when you have higher order polynomials that decompose into many variables, such as this:
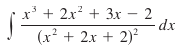
Also, some of these problems can get chalk full of substitutions, which further pulls one down into the algebra-trig tarpit. For example:
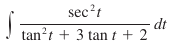
What is that?! Important calculus practice, or the author’s genuine concern for our attention-to-detail faculty? The problem with exercises like this is that it can easily burn through an hour of my time, leaving me frustrated, cursing at my desk full of eraser dust.
I’m prone to worrying that I don’t know a particular topic well enough, so can spend days churning through problems. Eventually I find myself on the brink of an aneurysm after spending an hour on a ‘calculus’ problem, realizing I’ve really just been practicing algebra, which means I’ve really just been accounting for minutiae of variables and radicals, and some momentary lapse of attention meant I wrote a + instead of a -.
So I doubt myself – am I missing something? Do I need to practice 100 more such problems until I don’t miss a detail? I love this stuff, so enjoy the grind. But time is precious. I’m not going to reach excellence if I spend a year toiling with grotesque polynomial trig integrals. I find myself torn between the pull for mastery and the push to move ahead and learn new things. With this being said (written), I now push forward to the next aneurysmal ledge…