Date Range: November 5 – November 10
Hours Spent:
14 hours:
- 5 hours on lectures and notes Professor Leonard – (Calculus 2 Lecture 9.3: Using the Integral Test for Convergence of Series; P-Series
- 9 hours on exercises (Thomas 13th ed, questions 1 – 34)
Summary:
Calculus 2 has basically been “here is an integration technique for integrating terms that you don’t yet know how to integrate” repeated over and over. Now I wade into series, and the story here is similar: “here’s a technique for determining convergence/divergence of a series that you don’t yet know how to determine” repeated again and again. So it is that I find myself with a series as unintimidating as
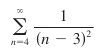
Where I can apply the divergence test and see that as n approaches infinity, that the series indeed equals 0. However, I need a new tool to confirm whether in fact it converges or not.
So it happens that if a series is positive, continuous, and decreasing (think a negative slope, i.e. derivative), like the above series is, then we can evaluate it using integration. If I find that its integral equals a finite value, then the series converges (otherwise it diverges). So, no problem, I can just apply the time-tested integration techniques I’ve been pounding into my skull for the last several months to find out if a series converges.
And while I’m at it, I learn about P-series, i.e. series of fractions that look like 1/n^p, where if p > 1, the series converge, or otherwise diverge. That helps out…and helps to add another layer of complexity to this beautiful subject.
Personal Observations:
- These get tricky as they involve logarithms, the mathematical constant, and trig functions (obviously!)
- For example:
here we pull out our integration techniques, like u substitution (ln n here) to find a trig identity and evaluate the integral with an arcsecant of a natural log – yes!!!
- I particularly had my brain mixed up with problems like this:
We first have to ask if it even passes the divergence test – well, does it? My instinct is to say ‘no’ because it’s a sine, i.e. a wave, so it can’t converge. But I need to prove it. This demanded some mental yoga, by converting x to 1/n and 1/n to x, then converting the limit from n to x as it reaches zero…yes, it diverges. But it took quite a bit of stretching and asking ‘wtf?!’ until I got it.
Reflections:
Working with series and thinking about convergence and divergence forces me to think in a different way from previous mathematical paradigms. At times I need to stop and look at a solution and marinate on how the different patterns and tools were used to understand whether a semi-intangible concept like infinite series closes is on a value, or is without end. It’s excellent mental exercise.