This is the last blog that was backlogged as a result of my website server blacklisting the Yogyakarta Special Region (and my too easily shelving the task until later). I’m currently in beautiful Vung Tau, Vietnam, a place I have returned to many times over the last 15 years (like Yogyakarta). There are no server issues here, so let’s go.
Up until now, I’ve worked with proper integrals – i.e. integrals taken between two fixed limits, where the function is continuous and uninterrupted between its limits (Calculus crawl-before-you-walk). Conversely, an improper integral occurs when one (or both) of the conditions for a proper integral is broken in the following way:
Infinite Interval – One or both of the bounds is infinite (then it’s not a bound, is it?). Take for example the following integral:
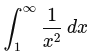
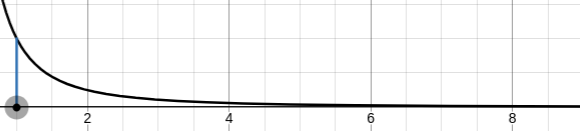
Here the upper bound is infinite. This leads to a curve-tail stretching infinitely to the right while tapering infinitely closer to 0. The following is a snapshot of that curve:
Infinite Discontinuity – There is a point within our curve where the denominator approaches zero (you can’t have zero in your denominator!) Take for example the similar integral:
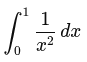
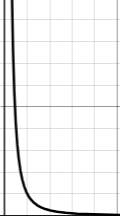
This results in a vertical asymptote, where the curve shoots off into space, while it infinitely tapers closer to the point where zero would exist in the denominator, like this:
To evaluate improper integrals, we replace problematic bounds with limit expressions. This allows us to study the behavior of a function as it approaches infinity (for the infinite intervals) or as it approaches the discontinuity point (in the case of the infinite discontinuities). Thus, our integrals look are transformed into
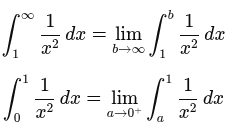
From here, we’re really just combining substitution with limit evaluation, and using our integration toolbag to solve more integrals. By evaluating our integral with our new substitute boundary, we’re better able to approximate the integral.
As we do this, we touch on the ideas of convergence/divergence that are forthcomingly expanded upon (I’m studying them now, in fact). Essentially, if a limit does in fact exist upon the evaluation of our integral, it’s said that the integral is convergent. That is, it converges upon a particular point. Alternatively, the integral diverges if the limit does not exist or tends toward infinity.
______________________________________________________________________________________________________________________
I know that what I’m writing about now is familiar to many, and has been better explained in numerous other publications, such as by Stewart or Thomas (the authors of the textbooks I learn with). While the purpose of these blogs is primarily to document my progress, they do serve me well in another way. Each of my lessons start out with lectures given by a teacher who explains the topics very well. I then move into the hard number crunching and practice until it makes sense. I then proceed to writing about it, thus bringing it back into the verbal thought process. This helps galvanize the information in question. And that’s a good thing, as there is so much of it that I can’t imagine how I’ll retain it all as I move forward. So, thank you hypothetical reader for helping me to learn and grow.