Date Range: November 24 – November 28
Hours Spent:
12.5 hours
- 5 hours on lectures and notes Professor Leonard – Calculus 2 Lecture 9.7: Power Series, Calculus of Power Series, Ratio Test for Int. of Convergence
- 7.5 hours on exercises (Thomas 13th ed, 10.5 questions 1 – 20, 37 – 45)
Summary:
Power series are infinite series in the form of
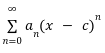
Where c is the center and are the coefficients. The standard form
is the special case centered at c = 0. Each power series has an interval of x-values for which the series converges; on this interval, the series defines a function. The interval of convergence is always centered at x = c and has a radius R. This size of R one of the following:
- R = 0; the series converges at x = c only
- R is infinite; the series converges for all values of x
- R is somewhere in between; the series converges absolutely for |x – c| < R (and all the can be differentiated or integrated)
Although we might know that the values within the radius converge, we need to test each endpoint of the radius for convergence. To do that, we typically apply the Ratio Test or the Root Test. It works like this:
- Apply the Ratio Test or Root Test to the general term
- Isolate the n’s and their limit by factoring out |x – c|
- Solve the resulting |x – c| < R
- Check for convergence at the endpoints
Two power series can have overlapping intervals of convergence. When this is the case, we can add, subtract, or multiply them term-by-term on the intersection of those intervals. This leads to the Cauchy Product, or Series Multiplication Theorem, which states that if two power series converge at |x| < R, then the product of those series also converges at |x| < R.
Personal Observations:
- Operations on power series were straightforward – it was essentially an application for the Ration Test and Root Test that we learned in the previous section.
- The Series Multiplication Theorem concept was confusing at first (and will probably still twist up my brain some when I encounter it again), but ultimately makes good sense, as power series are really just like polynomials, and so are operated on thus; the theorem ties it together with a convergence guarantee
- It seems to me that series will reappear quite a lot in the future, and, consequently, so to with the Cauchy Product
Reflections:
Each next step in my studies is essentially discovering out how what I just learned applies in greater context. This discovery then leads to the next, and the next, and so on. It’s all just a growing circle of light, of understanding of how it all interacts seamlessly. We never learn a concept and then leave it where we encountered it. It is part of our greater understanding, just as addition, the first of all mathematical lessons, is relevant in Power Series and the Cauchy Product, and how Power Series and the Cauchy Product will likely be an ever present fixture in all that is to follow.