Date Range: November 10 – November 15
Hours Spent:
14 hours
- 2.5 hours on lectures and notes Professor Leonard – Calculus 2 Lecture 9.4: The Comparison Test for Series and The Limit Comparison Test
- 11.5 hours on exercises (Thomas 13th ed, questions 1 – 40)
This unit, as the name implies, covers two comparisons that are used to determine convergence or divergence of a series. So I’ll break it down by comparison.
The Comparison Test for Convergence
This says that we can break a series up into pieces. One of those pieces will have dominant behavior (is it a logarithm, factorial, exponent, etc) that will shape the overall direction of the series. After breaking the series up into pieces , we can look for convergence/divergence. If the greater of the pieces converges, we can conclude that the series converges. Similarly, if the smaller piece diverges, we can conclude that the series also diverges. We can draw these conclusions because one factor will control the overall behavior of the series. For example:
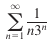
Here the exponent is the dominant force in the series. We can take (⅓)^n, recognize that it is a convergent series (|r| =⅓ < 1), and thus know that our series is also convergent as it is grows more quickly than the series it was drawn from.
The Limit Comparison Test
The Limit Comparison Test allows us to find convergence/divergence when we’re unable to with the simpler Direct Comparison Test. In essence, it says if the sum of a series and a partial sum have positive terms, and a limit exists for the quotient of the series and its partial sum, then both either converge or diverge. It takes more work than the Comparison Test, as we first take a partial sum, figure out if it converges or diverges, and then look for a limit in the relationship between the series and our partial sum . Overall, the same underlying ideas are shared with the Comparison Test, which is that we can tie behavior or pieces of a series to the series itself, and this can be most easily done by extracting the pieces that are easiest to evaluate and comparing them to their source.
Personal Observations:
- Working with logarithms in series was challenging for me. Their behavior and effect upon the series aren’t as easily evident, and manipulating series with them is more difficult
- It’s helpful to solve the same problem with different techniques, e.g. with direct comparison vs limit comparison, using L’Hopital’s, or integrating. The more I do this, the more I see they’re all interconnecgted.
- I can pull out partial sums that aren’t immediately evident in a series, such as in the following
Here I can pull 1/n^3/2 to perform a direct comparison, making for an easier evaluation than 1/n^2 (which at first seems the obvious choice)
Reflections:
Working with comparisons sheds light into phenomena in the world around me. Its underlying behavior is governed by, or described by the patterns I see in these series. I’m not so astute yet to give a specific, concrete example, but I sense it, I intuit it, which is satisfying.
I took extra time grinding through these problems. I could have done another 40, as I tripped up quite a few times. It’s been difficult to know which rules to use, which tools to use, etc. But I feel that they’ll make more sense as I push forward. I trust in the learning process. And I can’t wait to get to the next lesson.